Le tir dans le vide

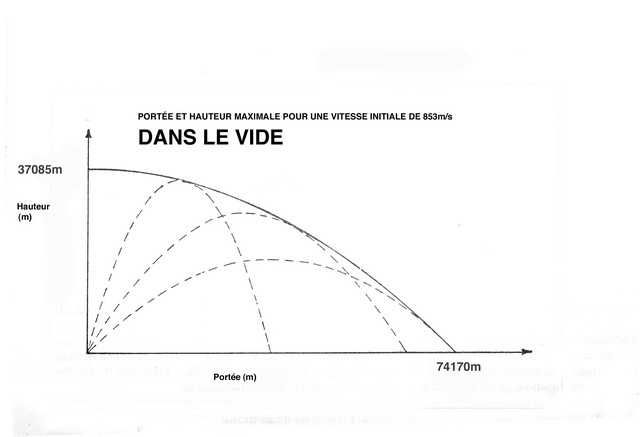
C’est la trajectoire théorique d’une balle, dans une ambiance où ne s’exerce aucun effort de résistance à l’avancement, mais où la pesanteur est bien présente. Le graphique ci-joint illustre cette situation. La hauteur et la portée atteintes ne dépendent que de la vitesse initiale qui a été communiquée au projectile. L’exemple correspond à une vitesse initiale de 853 m/s (2 800 fps) :

- la hauteur maximale que l’on peut atteindre dans le cas d’un tir vertical résulte du calcul suivant : (Vo x Vo)/(2 x 9,81) soit 37 085 m.

Dans les mêmes conditions, la portée maximale découle de la formule suivante : (Vo x Vo)/9,81 soit 74 170 m.

Cette situation, pour impressionnante qu’elle soit, est hautement irréaliste. Il est donc indispensable de se placer dans les conditions réelles.

 

Le tir sur la planète Terre

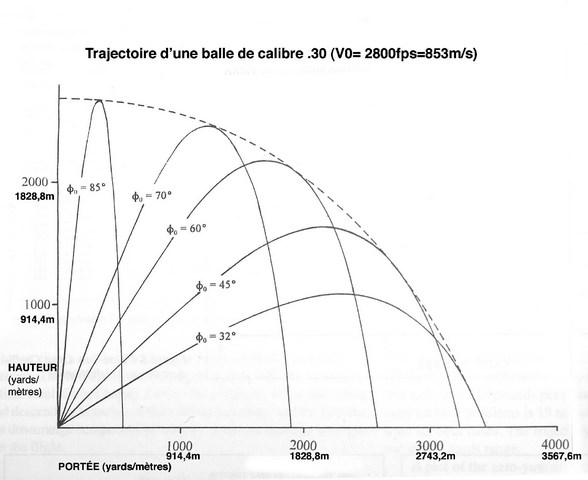
La résistance de l’air, ça existe et personne ne la conteste. Nous venons de voir la projection théorique, dans le vide, qui est particulièrement impressionnante. Pour illustrer nos propos, il suffit maintenant de jeter un coup d’œil au graphique 2, sur lequel 5 trajectoires sont représentées pour 5 angles de tir différents (32°, 45°, 60°, 70°, 85°). Ces trajectoires sont calculées grâce au logiciel « MCTraj » de Robert L. McCoy, pour une balle de calibre 7,62 mm (.30), dont la vitesse initiale est de 853 m/s (2 800 fps). La réalité saute aux yeux, même pour celui à qui les maths donnent de l’urticaire. La portée maximale est obtenue pour une valeur d’angle de 32°. Tout angle de tir, compris entre 0 et 90°, qui sera différent de cette valeur de 32° conduira donc à une portée forcément plus réduite. Intéressante aussi, la courbe en pointillés, qui délimite l’espace au-delà duquel un objectif ne pourra jamais être atteint. A l’évidence, tous les points compris entre les axes et cette courbe en pointillés seront atteignables. Les valeurs portées sur les axes donnent la hauteur et la portée maximale que peut atteindre le projectile dans les conditions réelles. Approximativement, on trouve une hauteur maximale de 2 500 mètres et une portée extrême de 3 200 mètres.

 

Conclusion

La présence de l’air ne laisse donc aucun doute sur son influence. Les résultats des deux tracés sont strictement comparables, puisque la vitesse initiale utilisée dans les deux cas est identique : 853 m/s. De 37 000 m théorique dans le vide intégral, la hauteur maximale est ramenée à 2 500 mètres, alors que la portée passe de 74 000 à 3 200 mètres… Ce n’est pas pour autant que le contexte est sécurisant, puisque, en supposant qu’un tireur soit autorisé à expédier son projectile dans toutes les directions autour de son poste, il serait susceptible d’atteindre tout point se situant à l’intérieur d’une ellipsoïde de 6,4 km de diamètre et de 2,5 km de haut. Vous voyez le genre ! Et puis, n’oublions pas de regarder ce qui se passe en fin de parcours d’une balle. Elle n’atterrit pas sur terre délicatement puisqu'elle est encore animée d’une vitesse non négligeable, donc d’une énergie qui peut être suffisante pour occasionner des blessures graves. D’après les essais et calculs, menés en Angleterre dans les années 1925, avec une cartouche réglementaire de 7,5 mm qui propulse un projectile de 11,27 g (174 grains) à une vitesse initiale de 792 m/s (2 600 fps), la portée maximale atteinte a été de 4 400 yards (4 023 m) pour un angle de tir d’environ 35°. A cette distance, la vitesse résiduelle du projectile est encore de 127 m/s (417 fps), ce qui est loin d’être anodin puisque cela représente 90 joules… c’est-à-dire l’énergie initiale d’une cartouche de 6,35 ! On comprend mieux la consigne permanente imposée au chasseur : le respect du tir fichant. Il en va de la sécurité de tous !